$ N^{3} $ 으로 삼각형 안에 점의 개수 구하는 방법입니다.
조건이 한 개 있는데 세 점이 같은 직선 위에 없을 때만 성립합니다.
좌표 평면에 점이 N개가 주어져 있다고 가정하겠습니다.
그럼 N개의 점 중에서 3점을 골라서 삼각형을 만들 수 있는 가짓수는
$ \binom{n}{3} $ 일 겁니다.
우리가 그럼 구하고자 하는 것은 각각 $ \binom{n}{3} $ 개의 삼각형 안에 들어있는 점의 개수 입니다.
어떻게 구하면 될까요...
삼각형을 구한 뒤 그 삼각형 안에 점의 개수를 일일히 세는 방법은 시간복잡도가 $ N^{4} $ 일겁니다.
$ N^{3} $ 으로 줄일려면 간단한 아이디어가 필요합니다.
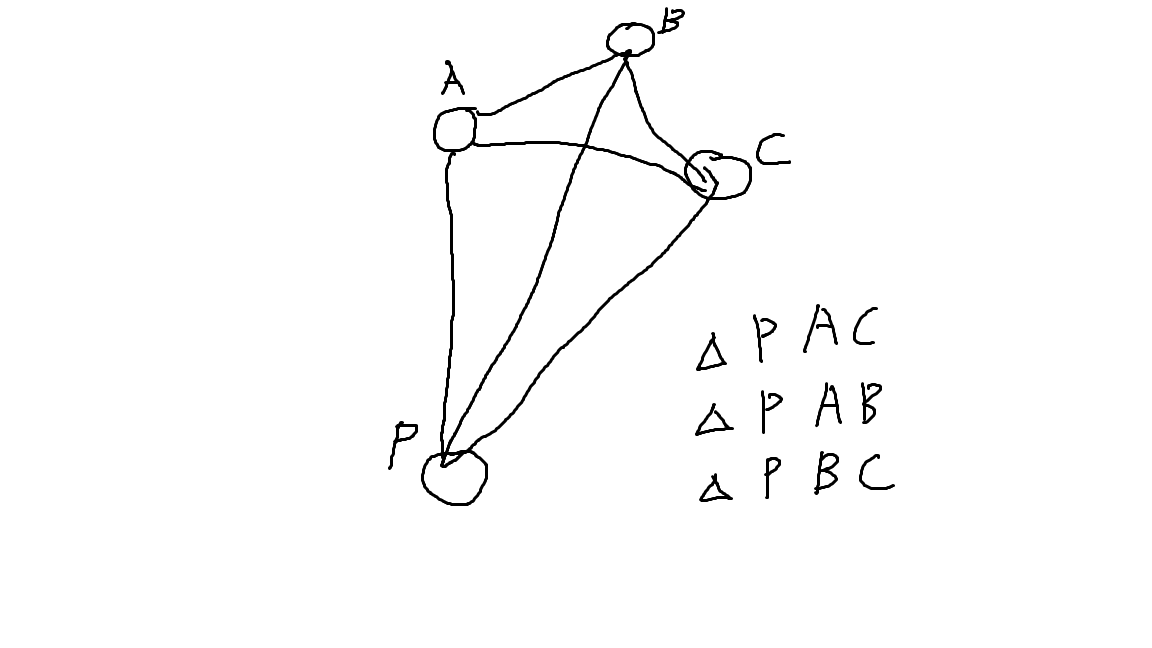
이렇게 $ PABC $ 사각형이 있다고 가정하겠습니다.
그리고 $ dp[A][B][C] $ 를 삼각형 $ ABC $ 안에 들어있는 점의 개수라고 했을 때
$ dp[A][B][C] = dp[P][A][B] + dp[P][B][C] - dp[P][A][C] $ 이 성립합니다.
즉 $ P $ 점을 고정한 채 $ dp[P][A][B] $ 값들을 미리 전처리 해 놓으면 $ dp[A][B][C] $ 는 $ O(1) $ 만에 구할 수 있습니다.
그럼 여기서 문제가 생깁니다. 어떤 $ P $ 를 고정시켜야 할까요?
$ x $ 좌표가 가장 왼쪽에 있거나 $ y $ 좌표가 가장 아래쪽에 있는 $ P $ 를 가져와야 계산이 편해집니다.
그럼 $ P $ 를 고정시켰습니다. 그럼 어떻게 해야 계산이 편해질까요?
제가 사용한 방법은 점들을 시계 방향으로 정렬합니다.
시계 방향으로 정렬하는 방법은 $ \underset{PA}{\rightarrow} $ 와 $ \underset{PB}{\rightarrow} $ 의 $ CCW $ 가 양수냐 음수냐로 정렬하면 되겠습니다.
그럼 당연히 $ \underset{PA}{\rightarrow}\ \underset{PB}{\rightarrow} \ \underset{PC}{\rightarrow} \ $ 이런 순서로 정렬되어졌다고 가정하면 점 $ B $ 는 $ PAC $ 안에 존재할 수 있는지 판별할 수 있게 됩니다.
이 경우에도 $ \underset{BA}{\rightarrow} $ 와 $ \underset{BC}{\rightarrow} $ 의 $ CCW $ 로 안에 존재하는 지 판별이 가능합니다.
이렇게 $ N^{3} $ 안에 $ dp[P][A][B] $ 를 구할 수 있습니다.
그럼 그 뒤에 $ dp[A][B][C] $ 도 비슷하게 구하면 되는데
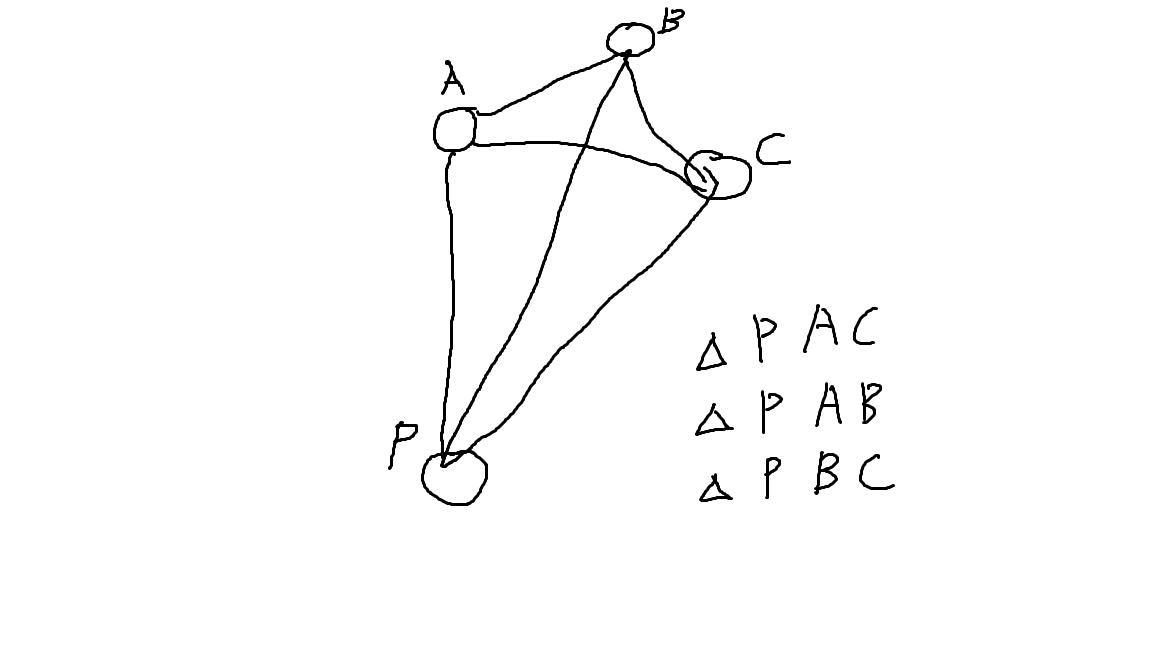
이런 식의 삼각형은 $ dp[A][B][C] = dp[P][A][B] + dp[P][B][C] - dp[P][A][C] $ 가 될테고
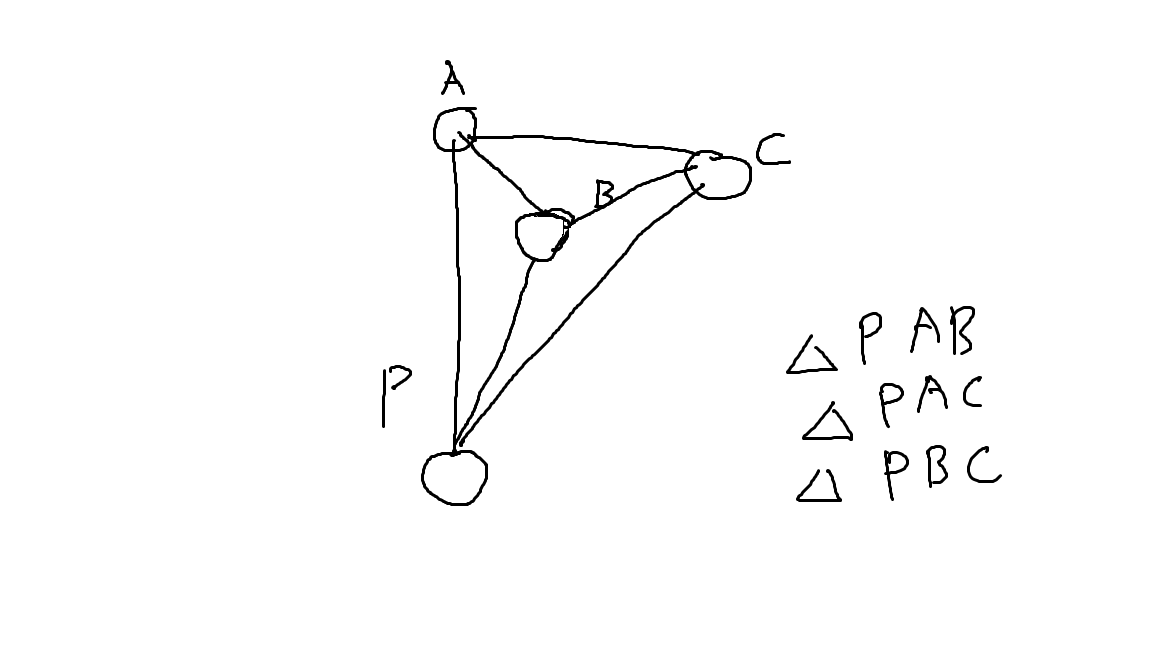
이런 식의 삼각형은 $ dp[A][B][C] = dp[P][A][C] - dp[P][A][B] - dp[P][B][C] - 1 $ 가 될겁니다.
추천 문제
https://www.acmicpc.net/problem/14164
'알고리즘' 카테고리의 다른 글
| Atcoder 문제 Brave CHAIN (0) | 2020.08.23 |
|---|---|
| Boj 8222 Distance (0) | 2020.08.22 |
| Codeforces Global Round 4 풀이 (0) | 2020.07.10 |
| Codeforces Global Round 9 풀이 (0) | 2020.07.05 |
| BCC 정점 기준으로 (0) | 2020.07.03 |