재밌는 문제들도 많았고 특히 오래달리기 저 문제를 통해 확장 유클리드를 공부할 수 있어서 좋았네요
Monotone 문제는 풀려있어서 풀지 않았습니다 ㅠ
1. 괄호
$ DP[x] $ 를 x 번째에서 끝나는 가장 긴 괄호의 개수라고 정의합시다.
그럼 stack 에 ( , { , [ 가 나타난 위치를 저장한 뒤 ) , } , ] 를 만날 때 스택에서 한 개를 pop 해줍니다.
그리고 pop 되어진거랑 지금 닫힌 문자랑 매칭되는 것이면 dp[pop 된 위치 - 1] + pop 된 문자열의 길이를 dp[현재 위치] 에다 저장해줍니다.
당연히 매칭이 안되면 스택을 그냥 초기화 시켜주면 됩니다.
2. 주식거래
그리디하게 풀 수 있습니다.
사는 경우에는 그 전의 주식의 값이 지금 주식의 값보다 크면 바꿔치기 합니다.
그러다가 그 전의 주식의 값이 지금 주식의 값보다 작으면 팝니다.
파는 경우에는 그 전의 주식의 값이 지금의 주식의 값보다 작으면 바꿔치기 합니다.
그러다가 그 전의 주식의 값이 지금의 주식의 값보다 크면 그 주식을 사는 경우로 바꿉니다.
그러면 최대로 많이 거래할 수 있습니다.
3. 전광판
2-sat을 알면 쉽게 풀 수 있습니다.
현재 전구가 켜져있으면 스위치 두 개를 다 쓰거나 안써야 됨으로
스위치 두 개를 각 각 $ A $ $ B $ 라고 하면
$ (A\vee B^{c}) \wedge (A^{c}\vee B) $ 이렇게 되어야 하고
현재 전구가 꺼져있으면 둘 중 하나만 써야 함으로
$ (A\vee B) \wedge (A^{c}\vee B^{c}) $ 이렇게 되어야 합니다.
각 각 경우에 간선을 추가 해준 뒤 2-sat 을 돌려줍니다.
저런 특수한 경우에선 union-find 로도 풀 수 있습니다.
Codeforces Round #309
이 라운드는 내가 치지는 않았다. 몇가지 이유가 있었는데 1) 시작할때 즈음 코포 서버가 난장판이어서 2) 문제가 mathy하다는 불안감이 계속 들어서 3) 내가 너무 졸려서... 정도. 일단 오늘 일어나
koosaga.com
4. Covernent
이 문제는 아직 못 풀었습니다. 풀면 업로드할 계획입니다.
MCMF 로 풀 수 있지만 리프 노드에서 출발할 때 어떻게 해야 리프 노드들의 lca 에서 flow가 끝나게 할 수 있는 지를 모르겠습니다... 풀 게 되면 업로드 하겠습니다.
5. Hanoi
큰 간판부터 거꾸로 봅니다.
지금 간판이 $ now $ 이고 그 다음으로 큰 간판을 $ next $ 라고 하겠습니다.
$ now $ 가 0 -> 1로 가야된다고 가정합시다.
그리고 0 -> 1 로 가는데 $ now $ 가 0에 있습니다.
그럼 $ next $ 는 0 -> 2 로 가야 $ now $ 가 0 -> 1로 움직일 수 있겠죠
$ now $ 가 1에 있는 경우는 $ next $ 가 0 -> 2로 간 뒤이니깐 이제 이 $ next $ 는 $ now $ 의 도착 지점으로 가야됨으로 행선지가 2 -> 1 로 되게됩니다.
이런 식으로 나머지 경우도 행선지를 정해주고 지금 위치가 이 행선지 구간에 없으면 최적의 경로가 아니라고 판단할 수 있습니다.
6. 오래달리기
$ S_{i} * x + D_{i} = L_{i} * y $ 이런 식이 $ n $ 개 주어져있습니다.
그럼 이 식을 다시 줄이면 $ S_{i} \equiv -D_{i} \ (mod \ L_{i}) $ 가 됩니다.
그런데 여기서 $ gcd(S_{i},L_{i}) $ 가 $ D_{i} $ 와 나눠 떨어지지 않으면 해가 존재 하지 않습니다.
하지만 그런 경우는 없다고 문제 조건에 제시되어 있으니 $ S_{i} \ L_{i} \ D_{i} $ 를 gcd 한 값으로 각 각 나눠줍니다.
그럼 $ S_{i} $ 의 $ L_{i} $ 에 대한 역원을 확장 유클리드로 구해주고 그 값을 $-D_{i} $ 에다 곱해줍니다.
$ x \equiv y \ (mod \ L_{i}) $ 식이 $ n $개가 나오게 됩니다.
그럼 이 식들을 포개주는 식으로 쭉 진행하면 답이 나오게 됩니다.
근데 답이 0 일 경우에는 문제 조건에 자연수를 출력하라고 명시되어있기에 모듈러를 한번 더해주고 출력하면 됩니다.
중국인 나머지 정리를 이용하면 더 쉬운 풀이가 될 수 있으나 제가 아직 공부하지 않아서 확장 유클리드로만 풀었습니다 ㅎㅎ...
참고 블로그
중국인의 나머지 정리 (Chinese Remainder Theorem) – The Casterian
예제 하나 문제) 다음 일차연립합동식을 만족하는 모든 $x$를 구하시오.\[ \begin{gather} x \equiv 5 \pmod{7} \\ x \equiv 13 \pmod{18} \\ x \equiv 21 \pmod{29} \end{gather} \] 풀이) $x$가 첫 번째 식을 만족해야 하므로 $x
casterian.net
7. Divisor
정수론 문제입니다... 문제를 풀다가 코포 문제를 푸는 듯한 착각이 들었네요
이 문제를 풀기 위한 아이디어 중 하나는 백 만 이하 숫자에서 가질 수 있는 약수의 최대값을 알면 문제 접근이 용이해집니다.
백 만 이하 숫자가 가질 수 있는 약수의 최대값을 어떻게 구할까요?
백 만 이하 숫자에서 가장 많은 소수들로 이루어진 숫자는 $ 2 * 3 * 5 * 7 * 11 * 13 * 17 $ 이고 7개가 가장 많습니다.
즉 $ 2^{7} $ 이 가장 많이 가질 수 있는 약수라는 것을 알 수 있습니다.
그럼 다시 문제로 돌아가서 배열의 숫자들을 받습니다.
그리고 vector<int> v[1000001] 이런 배열을 만듭니다.
그리고 그 배열의 숫자들의 약수를 구한 뒤 그 약수를 $ x $ 라고 하면 v[x] 에다가 그 배열의 위치 값을 추가해줍니다.
그리고 쿼리가 들어오는데 b 의 약수를 구해줍니다.
그리고 그 약수를 $ x $ 라고 하면 v[x] 에서 그 쿼리의 범위를 포함하고 있는 지를 lower_bound로 알아내면 됩니다.
그럼 여기서 드는 문제점이 쿼리가 들어오고 약수 구한 뒤 lower_bound 하면
$ O(Q*\sqrt{1e6}*log(N)) $ 이여서 20억 정도 돌지 않을까 하는 생각이 듭니다.
그런데 다시 생각해보면 lower_bound 는 약수의 개수만큼만 돌고 그 약수의 개수 최대값은 많아봐야 $ 2^{7} $ 이므로
실제 시간복잡도는 $ O(Q*(\sqrt{1e6} + 2^{7} * log(N))) $ 이 되서 2~3억번만 돌게 됩니다.
시간제한도 10초여서 충분히 통과할 수 있습니다.
8. 중심
문제 정확히 이해하는데 2시간이 걸렸습니다....
처음에 문제를 잘 못 이해해서 1시간 반 날리고
두 번째에는 70퍼센트 이해했지만 30퍼센트를 잘 못 이해했습니다.
제가 수식에 약해서 그런지 수식 디스크립션이 나오면 문제를 이해못하고 잘 못 이해하는게 제 스스로의 문제점이라고 생각합니다 ㅠㅠ ( 아까운 내 시간들 )
문제를 요약하자면 p 개의 정점을 가진 연결 그래프를 트리 안에서 만들어줍니다.
그럼 그 p 개의 정점에 속하지 않는 정점들 중 이 p 개의 정점을 가진 연결그래프로 가는 최단 경로 중 최댓값을 최소화 시키는 문제입니다 ( p 개의 정점을 가진 연결 그래프를 잘 만들어서.. )
이 문제를 풀 수 있는 가장 중요한 키는 리프 노드 순으로 봤을 때 무조건 위상 정렬처럼 되어야 한다는 것입니다.
왜냐하면 어떤 정점의 자식들이 다 체크가 안된 상태에서 올라가게 되면 p 개의 정점을 가진 그래프는 연결 그래프가 되지 못하기 때문이죠
즉 리프 노드 부터 차례대로 올라오면서 가장 작은 가중치 ( 리프노드가 아닌 점은 그 점으로 오는 리프노드와의 거리 중 최대값) 를 가진 것부터 처리해주면 됩니다. ( n-p 개까지만 돌려주면 됩니다 )
9. 자석
요즘들어 웰노운 문제가 되어버린 문제 유형입니다.
L 기준으로 오름 차순 정렬을 해준 뒤 뒤에것 부터 차례대로 봅니다.
$ dp[x] $ 는 $ x $ 막대기를 자석으로 만들면서 $ x $ ~ $ N $ 까지의 막대기가 문제 조건을 만족하도록 하는 공급된 전류의 최소값이라고 정의하겠습니다.
현재 구간의 R 보다 큰 L 은 현재 구간을 자석으로 만들어도 영향을 받지 않습니다.
이를 생각했을 때 문제가 하나 떠오릅니다.
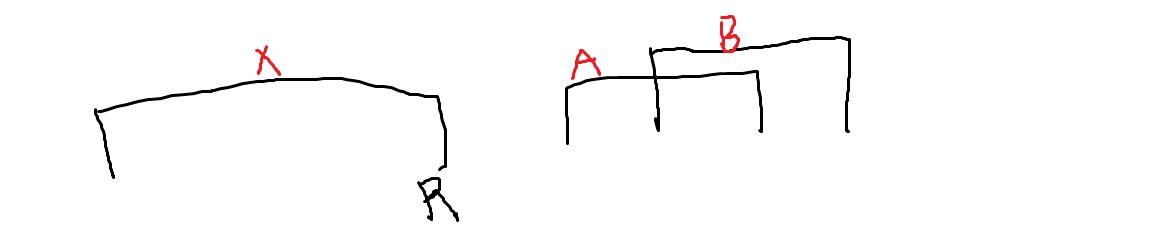
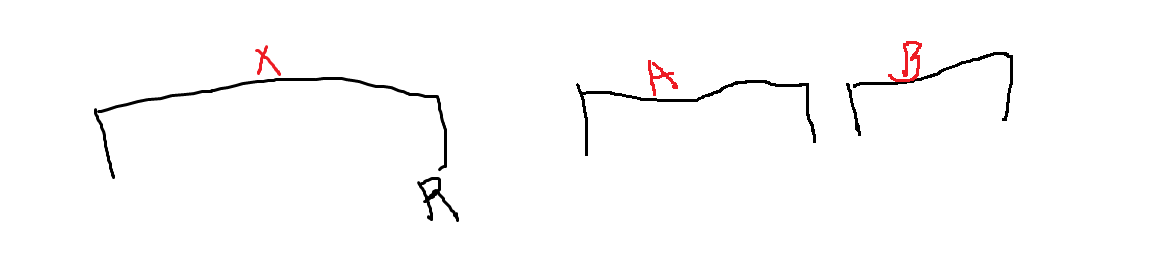
1번 경우는 $ dp[A] $ 와 $ dp[B] $ 중에서 최소 값을 가져와야 하지만
2번 경우는 무조건 $ dp[A] $ 값만 가져올 수 있습니다.
이 경우를 어떻게 따줘줘야 할까요?
$ S_R $ 를 $ x $ 의 $ R $ 보다 큰 $ L $ 를 갖는 $ x $ ~ $ N $ 번째 막대기의 $ R $ 의 최소값으로 정의합니다.
그럼 ($ x $ 의 $ R $) ~ $ S_R $ 사이에 있는 $ L $ 을 가진 막대기들은 어떤 막대기를 자석으로 바꿔도 다 붙게 됩니다.
즉 ($ x $ 의 $ R $) ~ $ S_R $ 사이에 있는 $ L $ 을 가진 막대기들의 $ dp $ 값 중 최소값 + $ x $ 의 $ w $ 를 $ dp[x] $ 에다 넣어줍니다.
그리고 답이 되는 경우는 $ 1 $ ~ $ N $ 중에서 가장 최소를 갖는 $ R $ 이 $ x $ 번째 막대기의 $ L $ 보다 크거나 같으면 그 $ dp[x] $ 는 답이 될 수 있는 경우이고 이 들 중 최소값을 출력해주면 됩니다.
'알고리즘' 카테고리의 다른 글
| 백준 1536번 Dance, Dance (0) | 2020.09.23 |
|---|---|
| 조금 신기한 분할정복 (0) | 2020.09.13 |
| SCPC 4회 1차 2차 예선 풀이 (0) | 2020.08.27 |
| Boj 11991. Fenced in (0) | 2020.08.24 |
| Atcoder 문제 Brave CHAIN (0) | 2020.08.23 |

