
ㅋㅋ 개 망했다.
A번 시페 당한게 너무 컸던 대회...
A. Searching Local Minimum [ SYSTEM FAILED!!! ]
살다살다 이분 탐색 코드를 잘못 짤 줄이야..
그리고 그게 프리테스트를 통과할 줄 이야..
이분 탐색을 했을 때 $ middle $ 값 과 $ middle - 1 $ , $ middle + 1$ 을 쿼리문 날려준다.
그랬을 때 $middle$ 값이 답이면 그냥 출력해주고 아니면 $middle - 1$ , $middle + 1$ 중 작은 값으로 이분 탐색을 진행한다.
이 문제에 대한 접근 힌트를 좀 하자면..
인터렉티브 문제는 이분 탐색으로 풀리는 경우가 매우 많다 ㅋㅋ
힌트 끗!
B1. Painting the Array I [ 79분 ]
A번에서 엄청 해메다 B 로 왔는데 난 개인적으로 B가 A보다 쉬웠던 것 같다..
A에서 좀 많이 해맸음..
일단 같은 색이 3개 이상 나오면 그 색은 사용하지 않는다고 한다.
3개 이상 나오면 무조건 0 과 1의 배열에 겹치게 나열될 것이기 때문이다.
그럼 연속된 색의 갯수가 최대 2개인 배열이 만들어지게 된다.
그랬을 때 배열이 진행되다가 연속된 색의 갯수가 2개인 걸 만났다고 가정하면
0과 1의 배열 모두에 포함되어 있을 것 이다.
그랬을 때 그 전이랑 같은 색의 연속된 색의 갯수가 2개인 걸 나중에 또 만나게 되면 지워야할 경우가 생길 수 있을 것이다.
예를 들어 그 색깔이 4라고 가정했을 때
44 xxxxxxx 44 이런 배열이고 x 로 이루어진 배열은 당연히 연속된 색이 없어야 한다.
그랬을 때 뒷쪽 44 중에 하나가 지워져야 할 경우는 0과 1 배열 둘 중에 하나에서 4가 계속해서 등장할 경우다.
즉 44 x 4 x 4 x 4 x 44 이런 경우일 것이다.
이런 경우만 판단해서 처리해주면 된다.
B2. Painting the Array II [ 97분 ]
일단 당연히 연속된 색은 다 지워주는게 이득일 것이고 그럼 연속되지 않는 색들의 배열이 만들어지게 된다.

A 와 A 끼리 합쳐지고 싶다고 가정하자.
그랬을 땐 당연히
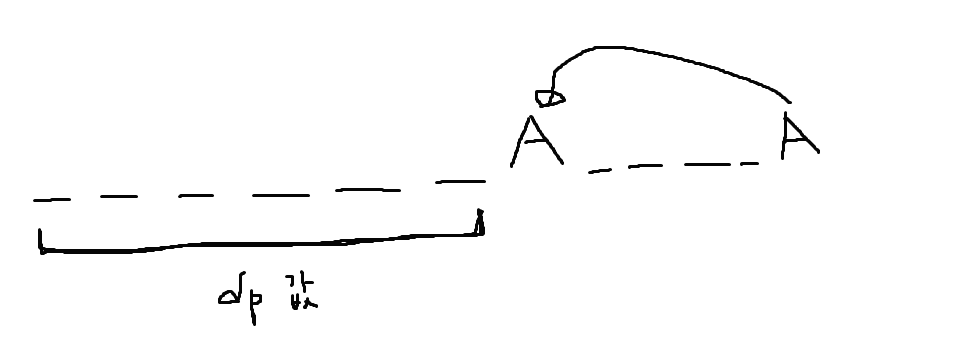
$ dp[i] $ 는 $ 1 \, \sim \, i \,$ 구간에서 지울 수 있는 최대값을 의미한다.
그럼 앞 쪽 A 의 위치가 $ j $ 라고 할 때 $ dp[j-1] \, + \, 1$ 이 답이 될 수 있고

그려보면 알겠지만 저 $ dp[j+1] \, + \, 1 $ 도 답이 될 수 있다.
### 후기
A에서 너무 삽질 했는데 그게 또 터져서 멘탈이 와그작 갈렸었다 ㅠ
근데 뭐 내가 풀 수 있는 데 까진 다 푼 것 같아서 괜찮기도 함..
C 번을 못 풀었는데 나중에 업솔빙을 할 계획이고 하게 되면 다시 올리도록 할 것이다.
D번도 풀어볼 수 있음 풀어봐야겠다..
근데 라운드 문제 자체는 재밌었음 약간 앳코더 느낌도 나면서 만족함 ㅋㅋ
'대회 > 코드포스' 카테고리의 다른 글
| Educational Codeforces Round 121 (Rated for Div. 2) 후기 (0) | 2022.01.18 |
|---|---|
| Codeforces Round #710 (Div. 3) (0) | 2021.03.26 |
| Educational Codeforces Round 103 (Rated for Div. 2) (0) | 2021.01.30 |


