AtCoder Regular Contest 112

 

YELLOW!!

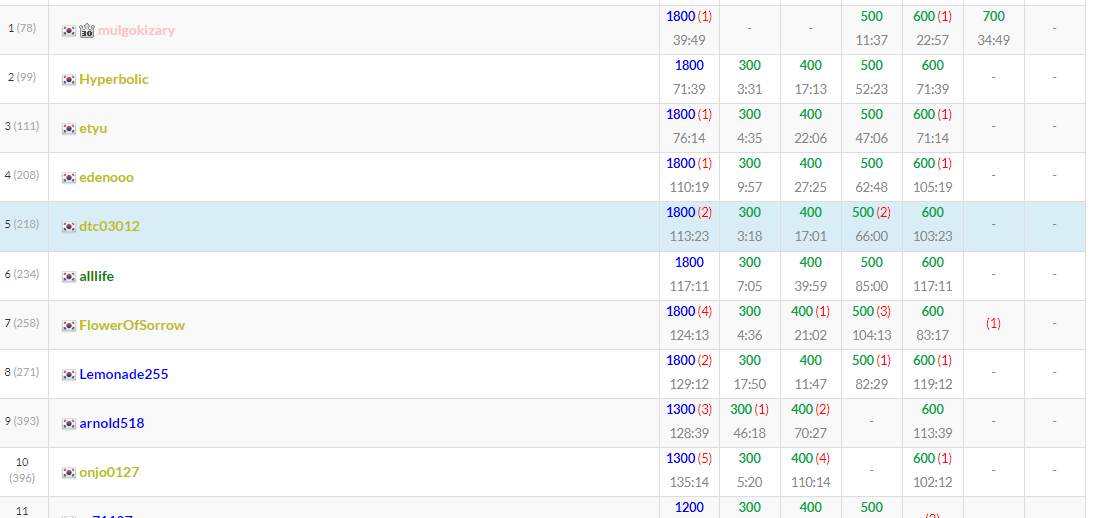
옐로를 찍었다! 옐로를 찍었다! 옐로를 찍었다! 옐로를 찍었다! 옐로를 찍었다!

 

A.  A - B = C   [ 3분 ]

 

요즘 뭔가 이런 유형이 자주 보이는 건 저 뿐인가요..?

$ A = B + C $ 로 바꾸어 봅시다.

그럼 $ B $ 와 $ C $ 가 $ L $ 일 때가 가장 최소 이고 그럼 $ A $ 는 $ 2*L $ 일때가 최소입니다.

그럼 $ A $ 가 $ 2*L $ 일 때는 한가지 경우가 존재하고

$ A $ 가 $ 2*L + 1 $ 일 때는 두가지 경우가 존재하고.. 이런 식으로 가게 될 겁니다.

이걸 $ A $ 가 $ R $ 일 때 까지 돌려주면 됩니다.

$ 2*L > R $ 일 때 조심!

 

 

 

B. - -- - B  [ 17분 ]

 

$ B $ 가  [ 0 ]  [ 음수 ]  [ 양수 ]  이 3가지 경우에 따라서 규칙을 찾으시면 됩니다.

직접 그려보면 됨으로 풀이는 PASS

 

 

 

C. DFS Game [ 66분 ]

 

개인적으로 좀 어려웠습니다.

 

Aoki 든 Taka 든 관계없이 처음에 이 루트 $ x $ 를 먹는 사람을  A 라 하고 아닌 사람을 B 라고 하겠습니다.

 

그럼 이 B 는 어떤 자식 노드로 갈 지를 정해줘야 됩니다.

 

그런데 보면 자식 노드의 갯수가 짝수면 다시 루트 $ x $ 로 올라왔을 때 순서가 유지되지만 홀수라면 순서가 뒤바뀌게 됩니다.

 

짝수 갯수의 서브트리를 생각해봅시다.

 

그 서브트리의 루트를 먹는 사람의 얻을 수 있는 코인을 $ c1 $  이라하고 나머지 사람이 먹을 수 있는 코인을 $ c2 $ 라고 하겠습니다.

 

그럼 $ c1 $ 이 $ c2 $ 보다 작으면 당연히 B 는 제일 처음에 이 짝수의 서브트리로 이동하는 것이 무조건 이득일 것입니다.

 

$ c1 $ 이 $ c2 $ 보다 크다면 당연히 서로 가는 걸 미루겠지요

 

그리고 홀수 갯수의 서브트리를 생각해봅시다.

 

어디로 가든 순서가 뒤바뀜으로 지금 결정권자는 무조건 $ c1 $ - $ c2 $ 가 작은 서브트리로 먼저갈려고 할 것입니다.

 

그렇게 홀수 갯수의 서브트리를 다 처리해준 다음 짝수 갯수의 서브트리에서 남은 거를 분배해주면 됩니다.

 

 

 

 D - Skate  [ 103분 ]

 

 

이런 테이블이 있습니다. 

 

각 행을 R1, R2, R3, R4 ... 로  정의하고

각 열을 C1, C2, C3, C4 ... 로  정의하겠습니다.

 

그럼 당연히 R1 과 C1 , Cn 은 서로 이동가능 할 것이고

Rm 과 C1, Cn 도 서로 이동가능 할 것입니다.

 

그리고 각 배열의 원소가 #  이고 이 위치가  ( x , y ) 이면

이 위치에서 갈 수 있는 행또는 열을 Direct 하게 이어줄 수 있습니다.

( 목적지 행 또는 열이 ( x , y ) 를 포함한 행 또는 열로 못갈 수 있기 때문 )

 

즉 SCC 를 해서 사이클을 만들어 줄 수 있고

 

모든 지점을 다 지나기 위해선 모든 행 또는 모든 열이 같은 사이클 안에 있어야 합니다.

 

즉 모든 행에서 $ distinct $ 한 사이클 갯수와 모든 열에서
$ distinct $ 한 사이클 갯수 중에서 최소값을 출력하면 됩니다.

 

 

 

E - Cigar Box   [ Upsolving ]

 

 

반대로 돌려준다고 생각하면 각각 왼쪽 오른쪽에서 집어서 아무 곳이나 보낸다고 생각할 수 있습니다.

 

그럼 지금 왼쪽에서 $ L $ 개 오른쪽에서 $ R $ 개를 집어서 기본 $permutation $ 자리에다 놓는다고 생각하겠습니다.

 

그럼 현재 진행한 $ operation $ 이 $ K $ 일 때 $ K \, - L \, -R $ 번의 $ operation $ 은 $ L + R $ 개 지점에서 왼쪽 오른쪽 아무 곳이나 움직일 수 있는 것입니다.

 

그렇다면 $ L + R $ 을 $ X $ 라고 하고 $ X $ 개의 공이 있다고 생각합니다.

 

$ X - 1 $ 의 공에서 한 개의 공을 추가한 횟수 + $ X $ 의 공에서 $ X $  개의 아무 공을 선택하는 횟수 * 2 가 그 다음 $ operation $ 의 값일겁니다.

 

그리고 $ L $ 과 $ R $ 일 때는 그 $ dp $  값 *  $ \binom{L+R}{L} $ 일 것입니다.

 

그럼 $ dp[x][y] $ 를  $ x $ 번 $ operation $ 을 하고 $ L + R $ 이 $ y $ 일 때 총 횟수라고 가정하면

 

$ dp[x][y]  = dp[x-1][y-1] + dp[x-1][y] * 2 * y $ 가 되게 됩니다.

 

그리고 난 뒤 각각 $ L $ 과 $ R $ 일 경우에 $ dp[M][L+R] $  * $ \binom{L+R}{L} $  값을 더해주면 됩니다

당연하게도 $ L + 1 $ 과 $ R - 1 $ 사이의 $ a_{i} $ 값들은 오름차순이여야 합니다.

 

 

 

 

###      후기

 

옐로를 찍었다!

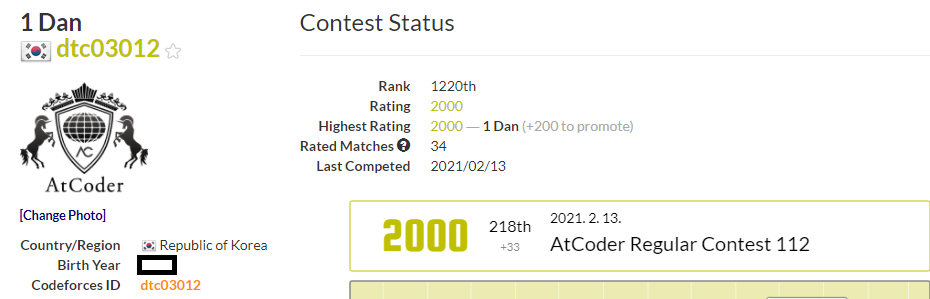
그것도 정확히 딱! 2000 점을 달성했습니다 ㅋㅋ

너무나도 기쁘네요.

개인적으로 앳코더 문제를 정말 좋아하는 사람으로써 저한테는 매우 의미가 있었습니다.

수학 공부를 좀 해야 유지를 할텐데 걱정이 많네요 ㅠㅠ

개인적으로 E 번 문제랑 C 번 문제는 좀 꿀잼이였습니다.

뭔가 앳코더 문제의 느낌이 요구하는 건 간단하거나 복잡하지 않은 데 그걸 유추해내가는 과정이 정말 어려운 것 같습니다.

이 대회 이후 탑코더를 또 처음 쳐보았습니다.

무슨 클래스를 정의해서 풀어야 하더군요... 디버깅 하는데 골치아팠습니다.. 처음이라..

4문제 나와서 4문제를 다 풀긴 했는데 1 번과 3 번이 코드에서 쓸데없는 부분이 많아서 오답처리 되버렸습니다..

제출하기 전에 뭐 30% 의 안쓰는 코드가 있으면.. 뭐라 뭐라 적혀있었는데 제대로 확인을 못한 제 잘못이죠 ㅠ

 

이로써 저도 백준 아이디에 노란색을 달 수 있게됬습니다!!

 

 

언젠간 이 모든 색깔이 시뻘건 색깔이 되기를 바라면서....